728x90
반응형
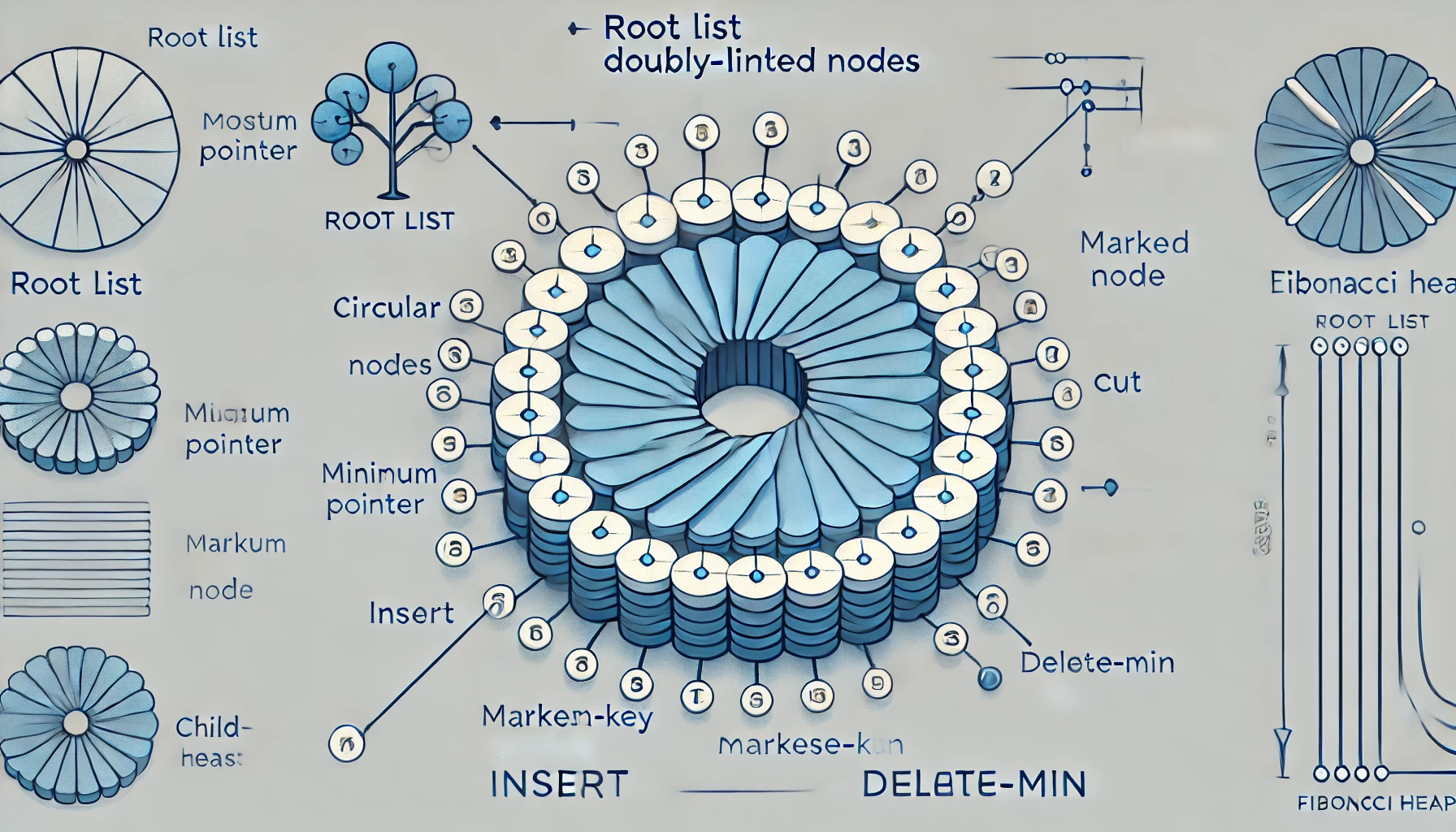
개요
Fibonacci Heap은 그래프 알고리즘에서 중요한 역할을 하는 우선순위 큐 구현 구조로, 특히 Decrease-Key, Merge 연산에서 탁월한 이론적 성능을 보이는 자료구조입니다. 이름은 노드 수가 피보나치 수열을 따르는 구조적 특성에서 유래하며, Dijkstra, Prim 알고리즘의 이론적 시간 복잡도를 낮추는 데 핵심 역할을 합니다.
1. 개념 및 정의
Fibonacci Heap은 연결 리스트 기반의 느슨한 구조로 구성된 **최소 힙(min heap)**이며, 여러 개의 트리를 루트 리스트로 구성하고 lazy 방식으로 병합 및 삽입을 처리합니다.
- 창시자: Fredman과 Tarjan (1984)
- 특징: 느슨한 균형 유지, 지연된 구조 조정(lazy consolidation)
- 용도: 최단 경로 탐색(Dijkstra), 최소 신장 트리(Prim) 등
2. 시간 복잡도
| 연산 | 시간 복잡도 | 설명 |
| Insert | O(1) (Amortized) | 새 노드를 루트 리스트에 추가 |
| Find-Min | O(1) | 최솟값 포인터로 직접 접근 |
| Union (Merge) | O(1) | 두 루트 리스트 연결 |
| Decrease-Key | O(1) (Amortized) | 자식 노드 분리 및 컷 수행 |
| Delete-Min | O(log n) (Amortized) | 최소 노드 제거 후 병합 수행 |
특히 Decrease-Key가 O(1)로 동작하는 점이 다른 힙 구조 대비 큰 장점입니다.
3. 구조적 특징
| 구성 요소 | 설명 | 예시 |
| 루트 리스트 | 연결 리스트 형태의 트리 헤드 노드 | 삽입/병합 시 직접 추가 |
| 마크 비트 | 자식이 분리된 노드 여부 표시 | 재귀적 컷 제어에 사용 |
| 최소 노드 포인터 | 전체 최소값을 가리키는 포인터 | Find-Min 연산 최적화 |
| 계수 속성 | 피보나치 수열 기반 자식 수 제한 | 계수 k일 때 자식 수 ≤ F(k+2) |
이러한 특성 덕분에 구조가 느슨해도 균형성과 성능이 보장됩니다.
4. 장점 및 단점
| 항목 | 장점 | 단점 |
| 성능 | 일부 연산의 O(1) 보장 | Delete 연산은 느릴 수 있음 |
| Merge 효율 | 힙 병합이 O(1)로 간단 | 코드 구현이 복잡함 |
| 그래프 알고리즘 적합 | Dijkstra, Prim 등에서 유리 | 실무 적용은 제한적임 |
이론적 성능은 우수하지만, 실제 응용에서는 더 단순한 자료구조가 선택되기도 합니다.
5. 활용 사례
| 분야 | 설명 | 예시 |
| 최단 경로 탐색 | 많은 Decrease-Key 호출 발생 | Dijkstra 알고리즘 개선 |
| MST (최소 신장 트리) | 노드 간 최소 간선 선택 | Prim 알고리즘 시간 단축 |
| 이론적 분석 | 복잡도 비교 기준용 | 힙 비교 실험의 기준 모델 |
Fibonacci Heap은 이론 연구와 고급 알고리즘 분석에 특히 활용됩니다.
6. 결론
Fibonacci Heap은 우선순위 큐 연산 중 일부를 최적 시간 복잡도로 구현할 수 있는 이론적 극한 구조입니다. 특히 그래프 알고리즘에서의 성능 분석과 효율 비교에 중요한 기준점이 되며, 다른 힙 구조보다 효율적인 연산을 제공하지만 구현이 복잡하고 캐시 효율이 떨어져 실제 시스템에서는 pairing heap, binary heap 등으로 대체되기도 합니다.
728x90
반응형
'Topic' 카테고리의 다른 글
| Count-min Sketch (0) | 2025.05.06 |
|---|---|
| KD-Tree(K-Dimensional Tree) (1) | 2025.05.06 |
| Splay Tree (0) | 2025.05.06 |
| DDR(Double Data Rate) 시리즈 (1) | 2025.05.06 |
| HBM(High Bandwidth Memory) 시리즈 (1) | 2025.05.06 |